Research Highlights
Collective Excitations & Light Induced Phases
Quantum materials exhibit non-universal properties that are the result of strong interactions between their constituents, defying a theoretical description in terms of free electrons. Their physical phenomena, such as superconductivity, long range entanglement and topologically protected currents, are exotic and absent in simple metals or insulator. This makes them promising candidates for applications in future quantum devices. While traditional methods to unravel these interesting phenomena in experiment include chemical doping, application of static pressure and magnetic fields, in recent years it has become possible to use ultra-short laser pulses to dynamically induce novel states and excitations in quantum materials.
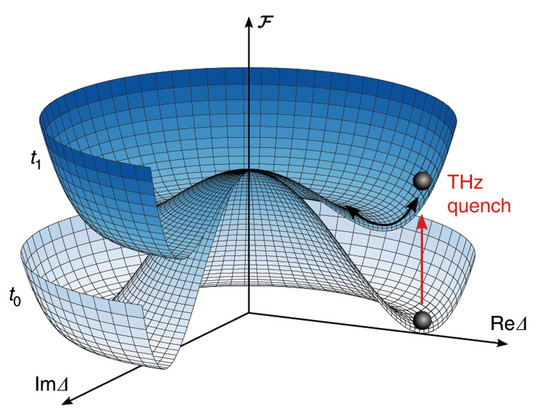
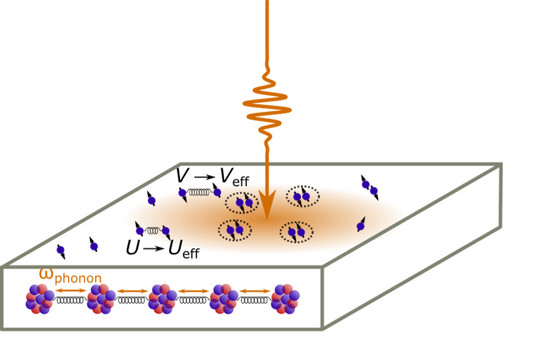
We theoretically investigated these phenomena for superconductors and heavy fermion systems using state-of-the-art numerical tools. By demonstrating how light induces Higgs oscillations we showed how the optical response of the superconductor can be used as spectroscopic tool to determine the underlying symmetry of the superconducting condensate [1,2]. We also demonstrated that long-range interactions can induce the stabilization of Higgs oscillations [3]. In the field of light induced phases we showed that non-equilibrium excitations can turn a charge density wave ordered system into a superconductor [4] and that short laser pulses can disentangle charge and magnetic order in a Kondo lattice system [5].
Digital Quantum Simulation on Modern Quantum Computers
Simulating quantum many-body systems is a key application for emerging quantum processors. Since Richard Feynman’s original proposal of a quantum computer various technologies have emerged as platforms for gate based quantum computing with the potential to outperform classical methods to simulate complex quantum systems. This is called the “quantum advantage”. Recent experiments by IBM claiming such utility have been refuted by more refined classical methods. Now the race is on to show a genuine quantum advantage.

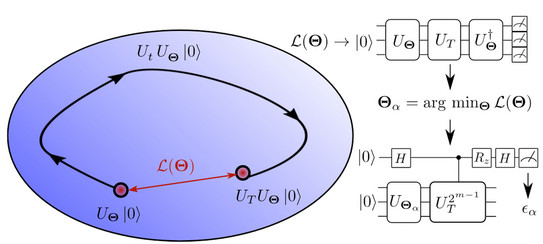
Besides platform enhancements, better quantum algorithms and error mitigation methods are key areas to achieve this aim. Our group investigated how error mitigation improves the simulation of non-equilibrium dynamics in spin and fermionic systems on a superconducting quantum computer [6] and we developed hybrid quantum algorithms to investigate time-periodic quantum systems [7]. Equipped with these tools we are now investigating more exotic quantum phases of matter, such as discrete time crystals and how to stabilize them on quantum devices [8].