Calendar

Location & approach

By car

The campus of TU Dortmund University is located close to interstate junction Dortmund West, where the Sauerlandlinie A 45 (Frankfurt-Dortmund) crosses the Ruhrschnellweg B 1 / A 40. The best interstate exit to take from A 45 is “Dortmund-Eichlinghofen” (closer to South Campus), and from B 1 / A 40 “Dortmund-Dorstfeld” (closer to North Campus). Signs for the university are located at both exits. Also, there is a new exit before you pass over the B 1-bridge leading into Dortmund.

To get from North Campus to South Campus by car, there is the connection via Vogelpothsweg/Baroper Straße. We recommend you leave your car on one of the parking lots at North Campus and use the H-Bahn (suspended monorail system), which conveniently connects the two campuses.

By train

TU Dortmund University has its own train station (“Dortmund Universität”). From there, suburban trains (S-Bahn) leave for Dortmund main station (“Dortmund Hauptbahnhof”) and Düsseldorf main station via the “Düsseldorf Airport Train Station” (take S-Bahn number 1, which leaves every 20 or 30 minutes). The university is easily reached from Bochum, Essen, Mülheim an der Ruhr and Duisburg.

You can also take the bus or subway train from Dortmund city to the university: From Dortmund main station, you can take any train bound for the Station “Stadtgarten”, usually lines U41, U45, U 47 and U49. At “Stadtgarten” you switch trains and get on line U42 towards “Hombruch”. Look out for the Station “An der Palmweide”. From the bus stop just across the road, busses bound for TU Dortmund University leave every ten minutes (445, 447 and 462). Another option is to take the subway routes U41, U45, U47 and U49 from Dortmund main station to the stop “Dortmund Kampstraße”. From there, take U43 or U44 to the stop “Dortmund Wittener Straße”. Switch to bus line 447 and get off at “Dortmund Universität S”.

By plane

The AirportExpress is a fast and convenient means of transport from Dortmund Airport (DTM) to Dortmund Central Station, taking you there in little more than 20 minutes. From Dortmund Central Station, you can continue to the university campus by interurban railway (S-Bahn). A larger range of international flight connections is offered at Düsseldorf Airport (DUS), which is about 60 kilometres away and can be directly reached by S-Bahn from the university station.

The H-Bahn (Suspended Monorail System)

The H-Bahn is one of the hallmarks of TU Dortmund University. There are two stations on North Campus. One (“Dortmund Universität S”) is directly located at the suburban train stop, which connects the university directly with the city of Dortmund and the rest of the Ruhr Area. Also from this station, there are connections to the “Technologiepark” and (via South Campus) Eichlinghofen. The other station is located at the dining hall at North Campus and offers a direct connection to South Campus every five minutes.

Map

The facilities of TU Dortmund University are spread over two campuses, the larger Campus North and the smaller Campus South. Additionally, some areas of the university are located in the adjacent “Technologiepark”.

Site Map of TU Dortmund University (Second Page in English).

ServicePortal UniMail

Contrast

Calendar

Location & approach

By car

The campus of TU Dortmund University is located close to interstate junction Dortmund West, where the Sauerlandlinie A 45 (Frankfurt-Dortmund) crosses the Ruhrschnellweg B 1 / A 40. The best interstate exit to take from A 45 is “Dortmund-Eichlinghofen” (closer to South Campus), and from B 1 / A 40 “Dortmund-Dorstfeld” (closer to North Campus). Signs for the university are located at both exits. Also, there is a new exit before you pass over the B 1-bridge leading into Dortmund.

To get from North Campus to South Campus by car, there is the connection via Vogelpothsweg/Baroper Straße. We recommend you leave your car on one of the parking lots at North Campus and use the H-Bahn (suspended monorail system), which conveniently connects the two campuses.

By train

TU Dortmund University has its own train station (“Dortmund Universität”). From there, suburban trains (S-Bahn) leave for Dortmund main station (“Dortmund Hauptbahnhof”) and Düsseldorf main station via the “Düsseldorf Airport Train Station” (take S-Bahn number 1, which leaves every 20 or 30 minutes). The university is easily reached from Bochum, Essen, Mülheim an der Ruhr and Duisburg.

You can also take the bus or subway train from Dortmund city to the university: From Dortmund main station, you can take any train bound for the Station “Stadtgarten”, usually lines U41, U45, U 47 and U49. At “Stadtgarten” you switch trains and get on line U42 towards “Hombruch”. Look out for the Station “An der Palmweide”. From the bus stop just across the road, busses bound for TU Dortmund University leave every ten minutes (445, 447 and 462). Another option is to take the subway routes U41, U45, U47 and U49 from Dortmund main station to the stop “Dortmund Kampstraße”. From there, take U43 or U44 to the stop “Dortmund Wittener Straße”. Switch to bus line 447 and get off at “Dortmund Universität S”.

By plane

The AirportExpress is a fast and convenient means of transport from Dortmund Airport (DTM) to Dortmund Central Station, taking you there in little more than 20 minutes. From Dortmund Central Station, you can continue to the university campus by interurban railway (S-Bahn). A larger range of international flight connections is offered at Düsseldorf Airport (DUS), which is about 60 kilometres away and can be directly reached by S-Bahn from the university station.

The H-Bahn (Suspended Monorail System)

The H-Bahn is one of the hallmarks of TU Dortmund University. There are two stations on North Campus. One (“Dortmund Universität S”) is directly located at the suburban train stop, which connects the university directly with the city of Dortmund and the rest of the Ruhr Area. Also from this station, there are connections to the “Technologiepark” and (via South Campus) Eichlinghofen. The other station is located at the dining hall at North Campus and offers a direct connection to South Campus every five minutes.

Map

The facilities of TU Dortmund University are spread over two campuses, the larger Campus North and the smaller Campus South. Additionally, some areas of the university are located in the adjacent “Technologiepark”.

Site Map of TU Dortmund University (Second Page in English).

ServicePortal UniMail

Physicist solved the puzzle of long ranged interactions between spins in In(Ga)As quantum dots

10/11/2022 -

in

Anders

Quantum dot ensemble

For a long time, the microscopic mechanism in In(Ga)As quantum dots ensemble was unclear that induces an effective long ranged interaction between the electron spins trapped in quantum dots. A team of theoretical solid-state physicists at the TU Dortmund has been able to solve this long standing puzzle and has published their results in the prestigious journal Physical Review Letters.

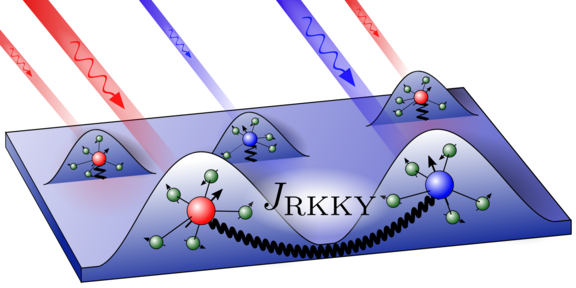
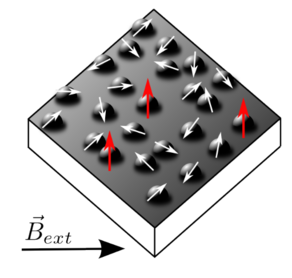
Quantum computers, unlike classical computers, utilised a superposition of quantum states. One approach to implement a qubit, the elementary unit of a quantum computer, is to confine spins, the magnetic moments of electrons, in semiconductor quantum dots and to use laser pulses to coherently control their alignments. In 2011, experiment on spins in In(Ga)As quantum dots showed that there is an interaction between the spins despite the large distance between the quantum dots [1]. "It is indispensable to understand this interaction in order to think about possible applications," Prof. Dr. Frithjof Anders explains. This might allow to control electronically the interaction strength.

Since the quantum dots are located on a wetting layer, which is formed during the sample fabrication process, the indirect Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction mediated via this layer became a promising candidate. The team proposed a new microscopic model based on charge fluctuations and calculated the effective distance dependent interaction strength between two spins using the numerical renormalization group method. The results were used
in an elaborate simulation of the spin dynamics in up to 10000 quantum dots. "We found a very good agreement between the experimental and theoretical results," Frederik Vonhoff summarizes.

[1] Spatzek et al., Phys. Rev. Lett. 107, 137402 (2011)

Frederik Vonhoff, Andreas Fischer, Kira Deltenre, and Frithjof B. Anders, Phys. Rev. Lett. 129, 167701 (2022)