Vortex Matter

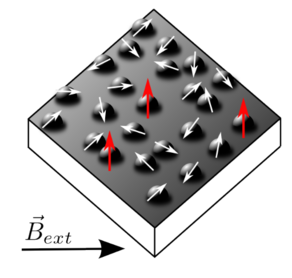
Type-I superconductors are both ideal conductors and perfect diamagnets. On the contrary, type-II superconductors exhibit a "mixed" physe for sufficiently strong magnetic fields, in which the magnetic flux can penetrate the sample in the form of quantized magnetic flux lines, which form the hexagonal Abrikosov vortex lattice. In this state, any external transport current leads to a Lorentz force and motion of flux lines which results in dissipation. Hence the perfect electric conductivity is lost. In high-Tc materials this field region covers essentially the whole superconducting phase (for an introduction into superconductivity, see Ref. [1], for a review on vortex physics in high-Tc superconductors, see Ref. [2]). To prevent dissipation, flux lines have to be pinned by impurities, which are an intrinsic property of (stochiometric) high-Tc materials but can also be engineered into the materials.

It has turned out that in high-Tc superconductors the vortex lattice is subject to fluctuations, which are both thermal fluctuations because type-II superconductivity and, thus, the vortex lattice exist up to relatively high temperatures and fluctuations from the frozen (quenched) impurities and defects. As a result, the vortex lattice constitutes a very interesting form of lattice matter, in which interactions are tunable (by magnetic field) and in which thermal and quenched disorder fluctuations give rise to a very rich phase diagram comprising both liquid and glassy phases. In a sense, the vortex matter can be regarded as "soft" because elastic deformations can be easily triggered by energies of the order of kBT or typical disorder energies, which makes vortex matter very susceptible to phase transformations. Because of this property, vortex matter has also shifted into the focus of statistical physics.

To prevent dissipation, flux lines have to be pinned by impurities. The presence of randomly distributed impurities leads to the formation of a glassy state of the flux line array, the "vortex glass", in which the linear resistivity of the superconductor vanishes because of arbitraryly high energy barriers between different metastable pinned states of the vortex lattice. Such glassy phases can be the result of point ("vortex glass") or columnar ("Bose glass") defects (see Refs. [2],[3] for recent reviews). The existence of vortex glass phases for point disorder has been proposed initially in Refs. [4], however, with the conclusion that these glassy phases lack any positional order.

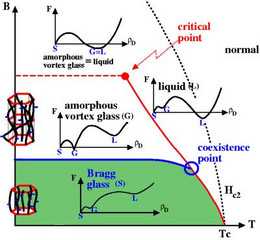
Since then, it has become clear that this picture should be modified in superconductors with point defects. The vortex glass phase which could be establisehd in these systems is actually a phase with quasi-long range topological order of the Abrikosov-lattice: The elastic "Bragg glass" [4]-[6]. It could be also called a "positional glass" since its properties are defined in terms of the vortex degrees of freedom. Moreover, thermal fluctuations of the vortex lines can give rise to a melting of the vortex lattice and, thus, the existence of "vortex liquid" phases (see [2] for a review).

It is the theoretical challenge in this field to develop a consistent theory for all types of vortex matter phases, including the quasi-ordered "Bragg glass", eventually another "amorphous vortex glass" phase lacking positional order, and the "vortex liquid" phases at higher temperatures. In order to achieve this we developed a unified theory of liquid and glassy vortex phases for superconductors containing quenched point disorder based on defect-mediated phase transitions between the different phases [7-11]. Specifically, we showed that the proliferation and pinning of dislocations and dislocation loops can explain the complex phase behavior observed in experiments [7-10]. We also studied dynamic features such as creep in a topologically disordered vortex glass containing dislocations [11].

Already for a single vortex line, the description of pinning-induced or thermal fluctuations and its depinning in reponse tu external currents is difficult because high-Tc materials are layered, and there exist both electromagnetic and Josephson coupling between vortex segments [12].

Columnar defects represent stronger pinning centers for vortex lines. At low concentrations of columnar defects several vortex lines compete for a single defect, which gives rise to a novel exchange-delocalization transition [13].

• [1] M. Tinkham, Introduction to Superconductivity, McGraw-Hill NY, 2nd edition 1996.
• [2] G. Blatter et al., Vortices in high-temperature superconductors, Rev. Mod. Phys. 66, 1125 (1994).
• [3] T. Nattermann and S. Scheidl, Vortex-glass phases in type-II superconductors, Advances in Physics 49, 607-704 (2000).
• [4] M.P.A. Fisher, Phys. Rev. Lett. 62, 1415 (1989), D.S. Fisher, M.P.A. Fisher, and D. Huse, Phys. Rev. B 43, 130 (1991). [5] T. Nattermann, Phys. Rev. Lett. 64, 2454 (1990).
• [6] T. Giamarchi and P.Le Doussal, Phys. Rev. Lett. 72, 1530 (1994), Phys. Rev. B 52, 1242 (1995).
• [7] J. Kierfeld, T. Nattermann, and T. Hwa, Topological order in the vortex glass phase of high-temperature superconductors, Phys. Rev. B 55, 626-629 (1997).
• [8] J. Kierfeld, Topological order in the phase diagram for high-temperature superconductors with point defects, Physica C 300, 171-183 (1998).
• [9] J. Kierfeld and V. Vinokur, Dislocations and the critical endpoint of the melting line of vortex line lattices, Phys. Rev. B 61, R14928-R14931 (2000).
• [10] J. Kierfeld, H. Nordborg, and V.M. Vinokur, Theory of Plastic Vortex Creep, Phys. Rev. Lett. 85, 4948-4951 (2000).
• [11] J. Kierfeld and V. Vinokur, Lindemann criterion and vortex lattice phase transitions in type-II superconductors, Phys. Rev. B 69, 024501 (2004).
• [12] J. Kierfeld, Single vortex fluctuations in type-II superconductors: Electromagnetic coupling and crossover to strong pinning, Phys. Rev. B 69, 144513 (2004).
• [13] J. Kierfeld and V.M. Vinokur, Competitive Localization of Vortex Lines and Interacting Bosons, Phys. Rev. Lett. 94, 077005 (2005).