Elastic shells, capsules, and polymer networks

Elastic shells are thin (quasi two-dimensional) elastic solids in a curved geometry. Of particular interest in soft matter theory and applications are closed spherical elastic shells, which can also be termed elastic capsules and which enclose a liquid of given volume or pressure. On the microscale, capsules have received a lot of attention as delivery systems and as biologically relevant model systems. Prominent examples of biological microcapsules are red blood cells or virus capsules; more generally, all biological cells where a thin layer of elastic cytoskeleton is surrounding the liquid cytosol and participating in deformations can be viewed as elastic capsules. If a coupling to the cytoskeleton is absent, a description of the membrane as a quasi two-dimensional liquid is more appropriate, and we obtain a vesicle rather than a microcapsule. Artificial capsules can be fabricated by various methods, for example, by interfacial polymerization at liquid droplets or by multilayer deposition of polyelectrolytes, and have numerous applications as delivery systems.

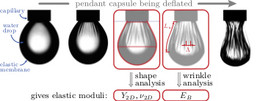
Usage as delivery systems requires that the mechanical behavior of capsule shells is understood and well characterized. In order to characterize microcapsules mechanically, their response to external forces and perturbations has to be explored quantitatively. For this purpose, we developed the method of “elastometry” for elastic capsules attached to a capillary, where we model the shape change of a hanging capsule during deflation, analogously to pendant drop tensiometry for liquid droplets.

Elastic instabilities such as buckling or wrinkling are relevant for the mechanical behavior of capsules as they give rise to stress concentration, for example, stress is concentrated in the rim of the indentation after buckling. Therefore, these instabilities represent potential pathways to failure of capsules in delivery applications. Moreover, elastic instabilities are fascinating from a theoretical point of view because they represent important shape bifurcations, which are characteristic for the polymorphism of many soft matter systems. The resulting buckled shapes of capsules can also be useful for colloidal self-assembly.

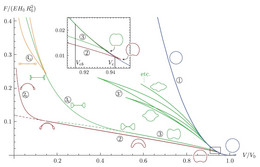
On the one hand, our research focuses on elastic instabilities such as the buckling instability and further post-buckling instabilities of spherical elastic shells. On the other hand, we are insterested in developing theoretical tools to enable the determination of elastic material parameters from analyzing experimental data on capsule shapes during a controlled capsule deformation.

Usage as delivery systems also requires controlled actuation of capsules. We investigated the manipulation of ferrofluid-filled capsules by magnetic fields and their deformation at liquid-liquid interfaces by surface tension.

Within the DFG Priority Programme SPP 1726 "Microswimmers" we also explore the use of elastic capsules as microswimmers.

References

• Buckling instability
  • Shallow shell theory of the buckling energy barrier: From the Pogorelov state to softening and imperfection sensitivity close to the buckling pressure
    L. Baumgarten and J. Kierfeld, Phys. Rev. E 99, 022803 (2019).
  • Buckling of thermally fluctuating spherical shells: Parameter renormalization and thermally activated barrier crossing
    L. Baumgarten and J. Kierfeld, Phys. Rev. E 97, 052801 (2018).
  • Buckling of spherical capsules
    S. Knoche and J. Kierfeld, Phys. Rev. E 84, 046608 (2011).
  • Secondary polygonal instability of buckled spherical shells
    S. Knoche and J. Kierfeld, EPL 106, 24004 (2014).
  • The secondary buckling transition: Wrinkling of buckled spherical shells
    S. Knoche and J. Kierfeld, Eur. Phys. J. E 37, 62 (2014).
  • Osmotic buckling of spherical capsules 
    S. Knoche and J. Kierfeld, Soft Matter 10, 8358-8369 (2014).
• Shape analysis
  • Pressure–deformation relations of elasto-capillary drops (droploons) on capillaries
    G. Ginot, F.S. Kratz, F. Walzel, J. Farago, J. Kierfeld, R. Höhler and W. Drenckhan, Soft Matter (2021).
  • Pendant Drop Tensiometry: A Machine Learning Approach
    F.S. Kratz and J. Kierfeld, J. Chem. Phys. 153, 094102 (2020).
  • Pendant capsule elastometry
    J. Hegemann, S. Knoche, S. Egger, M. Kott, S. Demand, A. Unverfehrt, H. Rehage, and J. Kierfeld, J. Colloid Interface Sci. 513, 549-565 (2018).
  • Elastometry of Deflated Capsules: Elastic Moduli from Shape and Wrinkle Analysis
    S. Knoche, D. Vella, E. Aumaitre, P. Degen, H. Rehage, P. Cicuta, and J. Kierfeld, Langmuir 29, 12463-12471 (2013).
• "Living" capsules
  • Material properties of interfacial films of mucoid and nonmucoid Pseudomonas aeruginosa isolates
    S.R. Balmuri, N.G. Waters, J. Hegemann, J. Kierfeld and T.H.R. Niepa, Acta Biomater. 118, 129-140 (2020).
• Actuation
  • Elastic capsules at liquid-liquid interfaces
    J. Hegemann, H.-H. Boltz and J. Kierfeld, Soft Matter 14, 5665-5685 (2018).
  • Strong deformation of ferrofluid-filled elastic alginate capsules in inhomogenous magnetic fields
    C. Wischnewski, E. Zwar, H. Rehage and J. Kierfeld, Langmuir 34, 13534-13543 (2018).
  • Spheroidal and conical shapes of ferrofluid-filled capsules in magnetic fields
    C. Wischnewski and J. Kierfeld, Phys. Rev. Fluids 3, 043603 (2018).

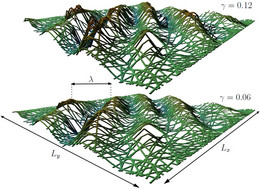
Quasi two-dimensional networks built from stiff semiflexible polymers are a particular realization of an elastic shell, which is of biological importance for the mechanical properties of the cytoskeletal cell cortex. We are studying elastic instabilities such as wrinkling for such polymer networks.

References

• Wrinkling of Random and Regular Semiflexible Polymer Networks
  P. Müller and J. Kierfeld, Phys. Rev. Lett. 112, 094303 (2014).